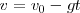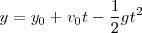Movimiento parabólico
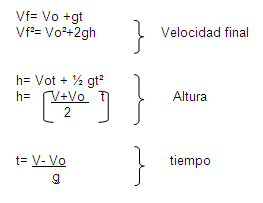
Se denomina movimiento parabólico al realizado por un objeto cuya trayectoria describe una parábola. Se corresponde con la trayectoria ideal de un proyectil que se mueve en un medio que no ofrece resistencia al avance y que está sujeto a un campo gravitatorio uniforme.
En realidad, cuando se habla de cuerpos que se mueven en un campo gravitatorio central (como el de La Tierra), el movimiento es elíptico. En la superficie de la Tierra, ese movimiento es tan parecido a una parábola que perfectamente podemos calcular su trayectoria usando la ecuación matemática de una parábola. La ecuación de una elipse es bastante más compleja. Al lanzar una piedra al aire, la piedra intenta realizar una elipse en uno de cuyos focos está el centro de la Tierra. Al realizar esta elipse inmediatamente choca con el suelo y la piedra se para, pero su trayectoria es en realidad un "trozo" de elipse. Es cierto que ese "trozo" de elipse es casi idéntico a un "trozo" de parábola. Por ello utilizamos la ecuación de una parábola y lo llamamos "tiro parabólico". Si nos alejamos de la superficie de la Tierra sí tendríamos que utilizar una elipse(como en el caso de los satélites artificiales).
EJEMPLOS
se patea un balón de fútbol con un ángulo de 37° con una
velocidad de 20 m/s. calcule:
a) la altura máxima.
b) el tiempo que permanece en el aire.
c) la distancia a la que llega al suelo.
d) la velocidad en x y y del proyectil después de 1 seg de
haber sido disparado
datos
ángulo = 37°
|
a) ymax = ?
|
d) vx =?
|
vo = 20m/s
|
b) t total = ?
|
vy = ?
|
g= -9.8 m/s^2
|
c) x = ?
|
paso 1
vox = vo cos a = 20 m/s cos 37° = 15.97 m/s
voy = vo se n a = 20 m/s sen 37° = 12.03 m/s
paso 2
calcular el tiempo de altura máxima , donde voy = 0
por lo tanto : t = (vfy - voy) / g = (0 - 12.03 m/s) / 9.8
= 1.22.seg.
paso 3
calcular a) la altura máxima:
ymax = voy t + gt^2 / 2= 12.03 m/s ( 1.22s) + (( -9.8m/s^2
)(1.22s)^2) / 2 = 7.38m
paso 4
calcular b) el tiempo total . en este caso solo se
multiplica el tiempo de altura máxima por 2, porque sabemos que la trayectoria
en este caso es simétrica y tarda el doble de tiempo en caer el proyectil de lo
que tarda en alcanzar la altura máxima.
t total = tmax (2) = 1.22s (2) = 2.44 s.
paso 5
calcular el alcance máximo, para lo cual usaremos esta
formula:
x = vx t total = 15.97 m/s ( 2.44s) = 38.96 m.
paso 6
vfy = gt + voy = (- 9.8) ( 1seg.) + 12.03 m/s = 2.23
m/s
vfx = 15.97 m/s ,ya que esta es constante durante
todo el movimiento.
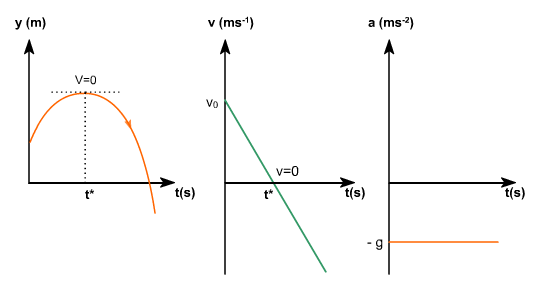
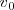es positiva, y así se mantendrá aún cuando su módulo llegue a valer cero. Esto ocurrirá en el punto más alto de la trayectoria, en el cual la 
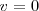, pues pasará de valores positivos a negativos. En ese punto de la altura máxima, el móvil se encontrará parado durante un instante, después del cual comenzará caer. Durante todo el movimiento la aceleración que sufrirá la partícula será la de la gravedad, la cual siempre tiene el mismo sentido, hacia abajo y, por convenio, negativo.
